|
||||||||||||
Linear
Feedback Shift Registers
|
| Brought to you by New Wave Instruments, the leading manufacturer of PN Sequence & PRBS Generators for use in the development of data communication, wireless, and spread spectrum systems. |
A linear feedback shift register (LFSR) is the heart of any digital system that relies on pseudorandom bit sequences (PRBS), with applications ranging from cryptography and bit-error-rate measurements, to wireless communication systems employing spread spectrum or CDMA techniques.
In this article we discuss the two implementations of LFSR generators, how to determine feedback taps for generating a maximal length sequence, and the properties of maximal length sequences (m-sequences). We also provide tables of m-sequence feedback taps.
LFSR Generator Implementations
Linear feedback shift registers can be implemented in two ways. The Fibonacci implementation consists of a simple shift register in which a binary-weighted modulo-2 sum of the taps is fed back to the input. (The modulo-2 sum of two 1-bit binary numbers yields 0 if the two numbers are identical, and 1 if the differ: 0+0=0, 0+1=1, 1+1=0.)
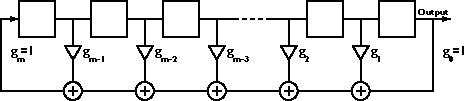
images/m_sequence_linear_feedback_shift_register_lfsr/Fibonacci_LFSR.gif
Figure 1. Fibonacci implementation of LFSR.
For any given tap, weight gi is either
0, meaning "no connection," or 1,
meaning it is fed back. Two exceptions are g0
and gm, which are always 1 and thus
always connected. Note that gm is not
really a feedback connection, but rather is the
input of the shift register. It is assigned a
feedback weight for mathematical purposes, as is
explained below.
The Galois implementation consists of a shift register, the contents of which are modified at every step by a binary-weighted value of the output stage.

images/m_sequence_linear_feedback_shift_register_lfsr/Galois_LFSR.gif
Figure 2. Galois implementation of LFSR.
Careful inspection reveals that the order of the
Galois weights is opposite that of the Fibonacci
weights.
Given identical feedback weights, the two LFSR implementations will produce the same sequence. However, the initial states of the two implementations must necessarily be different for the two sequences to have identical phase. The initial state of the Fibonacci form is called the initial fill or initial vector, and this initial fill comprises the first m bits output from the generator. The initial state of the Galois generator must be adjusted appropriately to attain the equivalent initial fill.
When implemented in hardware, modulo-2 addition is performed with exclusive-OR (XOR) gates. The Galois form is generally faster than the Fibonacci in hardware due to the reduced number of gates in the feedback loop, thus making it the favored form.
It should be noted that, in some industries, the Fibonacci form LFSR is referred to as a simple shift register generator (SSRG), and the Galois form is referred to as a multiple-return shift register generator (MRSRG) or modular shift register generator (MSRG).
Conventions for Feedback Tap Specification
A given set of feedback connections can be expressed in a convenient and easy-to-use shorthand form, with the connection numbers being listed within a pair of brackets. In doing so, connection g0 is implied, and not listed, since it is always connected. Although gm is also always connected, it is listed in order to convey the shift register size (number of registers).
A set of feedback taps for a Galois generator is denoted as
[f1, f2, f3, ..., fJ] g
where subscript J is the total number of feedback taps (not including g0), f1 = m is the highest-order feedback tap (and the size of the LFSR), and fj are the remaining feedback taps. The g subscript signifies the Galois LFSR form.
The set of feedback taps for the equivalent Fibonacci generator is denoted as
[f1, m-f2, m-f3, ..., m-fJ] f
where the f subscript signifies the Fibonacci LFSR form. Note that subtracting the feedback tap numbers from m is equivalent to reversing the order of the feedback taps (as they are defined in Figures 1 and 2).
As an example, consider an LFSR of size m = 8 with feedback connections at g8, g6, g5, g4, and implied g0. The feedback taps are specified as [8, 6, 5, 4]g for the Galois form, and [8, 8-6, 8-5, 8-4]f = [8, 2, 3, 4]f = [8, 4, 3, 2]f for the Fibonacci form. Note that the taps are customarily arranged in a descending order.
A set of feedback taps specified in this format is called a feedback tap set, feedback set, or feedback pattern.
It is important to recognize that feedback taps given in this shorthand form don't conform to the order of the weights given in Figure 1 for the Fibonacci generator. As such, it is best not to use Figures 1 and 2 in connection with this feedback convention. Rather, one should simply consider the first tap listed as being the output of the generator, the second tap being that just to the left of it, and so on, regardless of whether the generator is a Fibonacci or a Galois form.
In tables of m-sequence feedback sets, as presented below, neither the Fibonacci nor the Galois form is specified. This is because any given set will work with either implementation. If a given feedback set is used on both the Fibonacci and Galois forms, the sequence produced by one form will be the mirror image of the sequence produced by the other.
One other related convention should be mentioned: An LFSR with m shift register stages is said to be an Rm LFSR. For example, an R8 generator is one with eight stages. An alternative to this convention is PNm, or PN8 in this example. (PN is an acronym for pseudonoise, which is a term used in some industries for maximal length pseudorandom sequences, to be discussed next.)
Maximal Length Sequences
LFSR generators produce what are called linear recursive sequences (LRS) because all operations are linear. Generally speaking, the length of the sequence before repetition occurs depends upon two things, the feedback taps and the initial state. An LFSR of any given size m (number of registers) is capable of producing every possible state during the period N=2m-1, but will do so only if proper feedback taps, or terms, have been chosen. Such a sequence is called a maximal length sequence, maximal sequence, or less commonly, maximum length sequence. It is often abbreviated as m-sequence. In certain industries m-sequences are referred to as a pseudonoise (PN) or pseudorandom sequences, due to their optimal noise-like characteristics.
Maximal length generators can actually produce two sequences. One is the trivial one, of length one, that occurs when the initial state of the generator is all zeros. The other one, the useful one, has a length of 2m-1. Together, these two sequences account for all 2m states of an m-bit state register.
When the feedback taps of an LFSR are non-maximal, the length of the generated sequence depends upon the initial state of the LFSR. A non-maximal generator is capable of producing two or more unique sequences (plus the trivial all-zeros one), with the initial state determining which is produced. Each of these sequences is referred to as a state space of the generator. Together, all possible non-maximal sequences account for all 2m states of an m-bit state register.
Properties of non-maximal sequences are generally inferior to those of maximal sequences. So the use of non-maximal sequences in real systems is usually avoided in favor of their maximal-length counterparts.
Galois Field Mathematics and M-Sequences
Finite (Galois) field mathematics are used to derive m-sequence feedback taps. Any LFSR can be represented as a polynomial of variable X, referred to as the generator polynomial:
![]()
images/m_sequence_linear_feedback_shift_register_lfsr/generator_polynomial.gif
Equation 1. Generalized generator polynomial.
The coefficients gi represent the tap weights, as defined in Figures 1 and 2, and are 1 for taps that are connected (fed back), and 0 otherwise. The order of the polynomial, m, represents the number of LFSR stages. Rules of linear algebra apply to the polynomial, but all mathematical operations are performed in modulo-2:
Modulo-2 addition:
0 + 0 = 0
0 + 1 = 1
1 + 1 = 0
Modulo-2 multiplication:
0 * 0 = 0
0 * 1 = 0
1 * 1 = 1
As an example of polynomial representation, the generator polynomial
G(X) = X3 + X1 + 1
represents an LFSR with feedback taps 3 and 1, denoted as [3, 1]g:
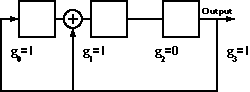
images/m_sequence_linear_feedback_shift_register_lfsr/LFSR_[3,1].gif
The constant 1 in the generator polynomial
represents the input connection of the shift
register, g0.
Now, here is the key to determining m-sequence feedback taps: The generator polynomial of Equation 1 is said to be primitive if it cannot be factored (i.e. it is prime), and if it is a factor of (i.e. can evenly divide) XN+1, where N = 2m-1 (the length of the m-sequence). It can be shown that an LFSR represented by a primitive polynomial will produce a maximal length sequence.
Consider again the example of the [3, 1]g LFSR just given. We wish to know if this generator will produce an m-sequence. First we note that m = 3 and N=23-1=7. It can be shown that its polynomial, X3+X1+1 , cannot be factored, and it can be shown that its polynomial is a factor of X7+1. Thus, we conclude that this LFSR will indeed produce a maximal length sequence.
In this example, we went through the process of determining whether or not the given set of feedback taps would result in a maximal length sequence. Normally, however, we are required to do just the opposite. That is, we are normally asked to find all sets of feedback taps that will produce m-sequences for a given register size.
For example, we may be asked to find all sets of maximal-length feedback taps for an LFSR with m=3 registers. We do this as follows: The length of the m-sequences will be N=23-1=7. We know that the solution lies in all the primitive factors of polynomial X7+1. We use modulo-2 linear algebra (perhaps with the aid of a computer algorithm) to find the prime factors to be
![]()
images/m_sequence_linear_feedback_shift_register_lfsr/polynomial_7.gif
The primitive polynomials are those factors whose order is the same as the register size, m = 3. Of the three prime factors, the last two meet this criterion. Thus we see that there are exactly two sets of m-sequence feedback taps, [3, 1]g and [3, 2]g.
It is interesting to note that, given any shift register size, there will always be an even number of m-sequence feedback sets. More specifically, given any one of its m-sequence feedback sets,
[f1, f2, f3, ..., fJ] g
there will be a companion set described as
[f1, m-f2, m-f3, ..., m-fJ] g
whose sequence will be the mirror image of the original set's sequence. Note that subtracting feedback tap numbers from m for the companion set is equivalent to reversing the order of those taps. Thus we conclude that, for any given feedback set that produces an m-sequence, the mirror image of the feedback set will produce the mirror image of the m-sequence. And, of course, the resulting sequence will also be an m-sequence since all possible states are exhausted. An astute reader may have noticed in the last example that the two derived sets of m-sequence feedback taps, [3, 1]g and [3, 2]g, are in fact mirror images of each other.
Tables of m-sequence feedback taps are presented below for the reader's convenience.
M-Sequence Properties
Properties of m-sequences include the following:
1. An m-bit register produces an m-sequence of period 2m-1.
2. An m-sequence contains exactly 2(m-1) ones and 2(m-1)-1 zeros.
3. The modulo-2 sum of an m-sequence and another phase of the same sequence yields yet a third phase of the sequence.
3a. (A corollary of 3.) Each node of an m-sequence generator runs through some phase of the sequence. (While this is obvious with a Fibonacci LFSR, it may not be with a Galois LFSR.)
4. A sliding window of length m, passed along an m-sequence for 2m-1 positions, will span every possible m-bit number, except all zeros, once and only once.
5. Define a run of length r to be a sequence of r consecutive identical numbers, bracketed by non-equal numbers. Then in any m-sequence there are:
1 run of ones of length m.
1 run of zeros of length m-1.
1 run of ones and 1 run of zeros, each of length m-2.
2 runs of ones and 2 runs of zeros, each of length m-3.
4 runs of ones and 4 runs of zeros, each of length m-4.
.
.
.
2m-3 runs of ones and 2m-3 runs of zeros, each of length 1.
6. If an m-sequence is mapped to an analog time-varying waveform, by mapping each binary zero to -1 and each binary one to +1, then the autocorrelation function will be unity for zero delay, and -1/(2m-1) for any delay greater that one bit, either positive or negative in time. The shape of the autocorrelation function between -1 bit and +1 bit will be triangular, centered around time 0. That is, the function will rise linearly from time = -(one-bit) to time 0, and then declines linearly from time 0 to time = +(one-bit).
Other interesting facts regarding m-sequences and feedback sets that produce them include the following:
1. If the order of the feedback taps (as defined in Figures 1 and 2) is reversed, the resulting sequence will be the time reversal of the original sequence, and will also be an m-sequence.
2. The tap numbers of any given m-sequence LFSR will all be relatively prime.
Tables of M-Sequence Feedback Taps
The following
tables contain m-sequence feedback sets for LFSR
sizes R3 through R32. The tables for R3 through
R24 contain all maximal feedback sets (except for
mirror image sequences). The tables for R25
through R32 contain maximal feedback sets for 2,
4, and 6 taps only. The last table contains a
sampling of "dense feedback sets"
(those with taps for at least half the stages)
for R25 through R32 registers.
The table files are in text format. However, the
files for R21 through R24 have been zipped for
faster downloading.
Not all feedback sets are explicitly listed in
the tables. Reversing the tap order for each
feedback set results in another valid m-sequence
feedback set. The sequence produced with the
reversed taps will be the mirror image of the
sequence produced with the original taps. If the
original feedback set is [m, A, B, C], the
reversed feedback set is described by [m, m-C,
m-B, m-A], where m is the number of LFSR stages.
3 Stages 3 stages, 2 taps: (1 set)[3, 2] 11 Stages11 stages, 2 taps: (1 set) [11, 9] 11 stages, 4 taps: (22 sets) [11, 10, 9, 7] [11, 10, 9, 5] [11, 10, 9, 2] [11, 10, 8, 6] [11, 10, 8, 1] [11, 10, 7, 3] [11, 10, 7, 2] [11, 10, 6, 5] [11, 10, 4, 3] [11, 10, 3, 2] [11, 9, 8, 6] [11, 9, 8, 4] [11, 9, 8, 3] [11, 9, 7, 4] [11, 9, 7, 2] [11, 9, 6, 5] [11, 9, 6, 3] [11, 9, 5, 3] [11, 8, 6, 4] [11, 8, 6, 3] [11, 7, 6, 5] [11, 7, 6, 4] 11 stages, 6 taps: (40 sets) [11, 10, 9, 8, 7, 4] [11, 10, 9, 8, 7, 1] [11, 10, 9, 8, 5, 4] [11, 10, 9, 8, 4, 3] [11, 10, 9, 8, 3, 1] [11, 10, 9, 7, 5, 1] [11, 10, 9, 7, 4, 1] [11, 10, 9, 6, 5, 4] [11, 10, 9, 6, 4, 2] [11, 10, 9, 6, 3, 1] [11, 10, 9, 6, 2, 1] [11, 10, 9, 5, 4, 3] [11, 10, 9, 5, 4, 1] [11, 10, 9, 5, 3, 1] [11, 10, 9, 4, 3, 2] [11, 10, 8, 7, 6, 5] [11, 10, 8, 7, 6, 3] [11, 10, 8, 7, 5, 3] [11, 10, 8, 7, 4, 1] [11, 10, 8, 6, 5, 4] [11, 10, 8, 6, 5, 1] [11, 10, 8, 6, 4, 3] [11, 10, 8, 6, 4, 2] [11, 10, 8, 5, 3, 2] [11, 10, 8, 4, 3, 2] [11, 10, 7, 6, 5, 3] [11, 10, 7, 6, 5, 1] [11, 10, 7, 6, 4, 2] [11, 10, 7, 6, 4, 1] [11, 10, 7, 6, 3, 2] [11, 10, 7, 4, 3, 2] [11, 9, 8, 7, 6, 3] [11, 9, 8, 7, 4, 2] [11, 9, 8, 6, 5, 2] [11, 9, 8, 6, 4, 3] [11, 9, 7, 6, 5, 4] [11, 9, 7, 6, 5, 3] [11, 9, 7, 6, 4, 2] [11, 9, 6, 5, 4, 3] [11, 8, 7, 6, 4, 3] 11 stages, 8 taps: (25 sets) [11, 10, 9, 8, 7, 6, 5, 3] [11, 10, 9, 8, 7, 6, 5, 2] [11, 10, 9, 8, 7, 6, 4, 1] [11, 10, 9, 8, 7, 6, 3, 2] [11, 10, 9, 8, 7, 5, 4, 2] [11, 10, 9, 8, 7, 5, 3, 2] [11, 10, 9, 8, 7, 5, 2, 1] [11, 10, 9, 8, 7, 4, 3, 1] [11, 10, 9, 8, 7, 4, 2, 1] [11, 10, 9, 8, 6, 5, 4, 2] [11, 10, 9, 8, 6, 5, 3, 2] [11, 10, 9, 8, 6, 5, 3, 1] [11, 10, 9, 8, 6, 4, 3, 2] [11, 10, 9, 8, 5, 4, 2, 1] [11, 10, 9, 7, 6, 5, 4, 3] [11, 10, 9, 7, 6, 5, 4, 1] [11, 10, 9, 7, 6, 4, 3, 2] [11, 10, 9, 7, 5, 4, 3, 1] [11, 10, 9, 6, 5, 4, 3, 2] [11, 10, 9, 6, 5, 4, 3, 1] [11, 10, 8, 7, 6, 5, 4, 2] [11, 10, 8, 7, 6, 4, 3, 1] [11, 10, 8, 7, 5, 4, 3, 2] [11, 9, 8, 7, 6, 5, 3, 2] [11, 9, 8, 7, 6, 4, 3, 2] 19 Stages 27 Stages 4 Stages4 stages, 2 taps: (1 set)[4, 3] 12 Stages12 stages, 4 taps: (9 sets) [12, 11, 10, 4] [12, 11, 10, 2] [12, 11, 8, 6] [12, 11, 7, 4] [12, 10, 9, 3] [12, 10, 5, 4] [12, 9, 8, 5] [12, 9, 7, 6] [12, 8, 6, 5] 12 stages, 6 taps: (43 sets) [12, 11, 10, 9, 8, 4] [12, 11, 10, 9, 6, 4] [12, 11, 10, 9, 6, 2] [12, 11, 10, 9, 4, 3] [12, 11, 10, 9, 4, 2] [12, 11, 10, 8, 7, 3] [12, 11, 10, 8, 7, 2] [12, 11, 10, 8, 6, 4] [12, 11, 10, 8, 6, 1] [12, 11, 10, 8, 5, 1] [12, 11, 10, 8, 2, 1] [12, 11, 10, 7, 6, 3] [12, 11, 10, 7, 6, 2] [12, 11, 10, 7, 5, 2] [12, 11, 10, 7, 2, 1] [12, 11, 10, 6, 3, 2] [12, 11, 9, 8, 7, 6] [12, 11, 9, 8, 7, 4] [12, 11, 9, 8, 4, 1] [12, 11, 9, 8, 3, 1] [12, 11, 9, 7, 6, 5] [12, 11, 9, 7, 6, 4] [12, 11, 9, 7, 3, 1] [12, 11, 9, 6, 5, 3] [12, 11, 9, 5, 4, 1] [12, 11, 8, 7, 6, 3] [12, 11, 8, 7, 5, 4] [12, 11, 8, 6, 5, 2] [12, 11, 8, 5, 4, 2] [12, 11, 7, 5, 4, 3] [12, 11, 6, 4, 3, 2] [12, 10, 9, 8, 7, 6] [12, 10, 9, 8, 7, 3] [12, 10, 9, 8, 6, 2] [12, 10, 9, 8, 4, 3] [12, 10, 9, 8, 4, 2] [12, 10, 9, 7, 5, 2] [12, 10, 9, 6, 4, 3] [12, 10, 9, 6, 4, 2] [12, 10, 8, 7, 6, 2] [12, 9, 8, 7, 5, 3] [12, 9, 8, 7, 4, 3] [12, 9, 8, 6, 5, 4] 12 stages, 8 taps: (18 sets) [12, 11, 10, 9, 8, 7, 6, 3] [12, 11, 10, 9, 8, 7, 4, 3] [12, 11, 10, 9, 8, 6, 5, 4] [12, 11, 10, 9, 8, 5, 2, 1] [12, 11, 10, 9, 8, 4, 3, 1] [12, 11, 10, 9, 7, 6, 5, 1] [12, 11, 10, 9, 7, 3, 2, 1] [12, 11, 10, 9, 6, 5, 4, 1] [12, 11, 10, 9, 6, 5, 2, 1] [12, 11, 10, 8, 6, 5, 4, 2] [12, 11, 10, 8, 6, 4, 3, 1] [12, 11, 10, 7, 6, 5, 4, 1] [12, 11, 10, 7, 5, 4, 3, 1] [12, 11, 9, 8, 7, 6, 4, 1] [12, 11, 9, 7, 6, 5, 4, 2] [12, 11, 8, 7, 5, 4, 3, 2] [12, 10, 9, 8, 7, 5, 3, 2] [12, 10, 9, 8, 6, 5, 4, 2] 12 stages, 10 taps: (2 sets) [12, 11, 10, 9, 8, 7, 5, 4, 3, 2] [12, 11, 10, 9, 8, 7, 5, 4, 3, 1] 20 Stages 28 Stages 5 Stages5 stages, 2 taps: (1 set)[5, 3]5 stages, 4 taps: (2 sets)[5, 4, 3, 2] [5, 4, 3, 1] 13 Stages13 stages, 4 taps: (33 sets) [13, 12, 11, 8] [13, 12, 11, 2] [13, 12, 11, 1] [13, 12, 10, 9] [13, 12, 10, 6] [13, 12, 10, 3] [13, 12, 9, 7] [13, 12, 9, 3] [13, 12, 8, 2] [13, 12, 7, 6] [13, 12, 7, 5] [13, 12, 7, 4] [13, 12, 6, 3] [13, 12, 4, 3] [13, 12, 4, 2] [13, 11, 10, 6] [13, 11, 10, 5] [13, 11, 9, 8] [13, 11, 9, 5] [13, 11, 8, 7] [13, 11, 8, 6] [13, 11, 8, 4] [13, 11, 8, 3] [13, 11, 7, 2] [13, 11, 5, 4] [13, 11, 4, 3] [13, 10, 9, 4] [13, 10, 8, 5] [13, 10, 8, 3] [13, 10, 7, 6] [13, 10, 6, 5] [13, 10, 6, 4] [13, 8, 7, 6] 13 stages, 6 taps: (118 sets) [13, 12, 11, 10, 9, 6] [13, 12, 11, 10, 9, 3] [13, 12, 11, 10, 9, 2] [13, 12, 11, 10, 8, 7] [13, 12, 11, 10, 8, 6] [13, 12, 11, 10, 8, 5] [13, 12, 11, 10, 8, 1] [13, 12, 11, 10, 7, 1] [13, 12, 11, 10, 5, 2] [13, 12, 11, 10, 5, 1] [13, 12, 11, 10, 4, 2] [13, 12, 11, 10, 4, 1] [13, 12, 11, 10, 3, 2] [13, 12, 11, 9, 8, 4] [13, 12, 11, 9, 7, 3] [13, 12, 11, 9, 6, 5] [13, 12, 11, 9, 6, 4] [13, 12, 11, 9, 5, 3] [13, 12, 11, 9, 2, 1] [13, 12, 11, 8, 7, 5] [13, 12, 11, 8, 7, 2] [13, 12, 11, 8, 7, 1] [13, 12, 11, 8, 5, 4] [13, 12, 11, 8, 4, 1] [13, 12, 11, 8, 3, 1] [13, 12, 11, 8, 2, 1] [13, 12, 11, 7, 6, 5] [13, 12, 11, 7, 6, 3] [13, 12, 11, 7, 5, 4] [13, 12, 11, 7, 5, 1] [13, 12, 11, 6, 5, 4] [13, 12, 11, 6, 5, 3] [13, 12, 11, 6, 4, 3] [13, 12, 11, 6, 3, 1] [13, 12, 11, 5, 4, 1] [13, 12, 11, 4, 3, 2] [13, 12, 10, 9, 8, 6] [13, 12, 10, 9, 8, 5] [13, 12, 10, 9, 8, 2] [13, 12, 10, 9, 7, 4] [13, 12, 10, 9, 6, 4] [13, 12, 10, 9, 6, 3] [13, 12, 10, 9, 5, 2] [13, 12, 10, 9, 3, 1] [13, 12, 10, 8, 7, 5] [13, 12, 10, 8, 6, 2] [13, 12, 10, 8, 5, 4] [13, 12, 10, 8, 5, 2] [13, 12, 10, 8, 3, 2] [13, 12, 10, 7, 6, 3] [13, 12, 10, 7, 5, 2] [13, 12, 10, 7, 4, 3] [13, 12, 10, 7, 4, 1] [13, 12, 10, 6, 5, 3] [13, 12, 10, 6, 3, 2] [13, 12, 9, 8, 7, 6] [13, 12, 9, 8, 6, 4] [13, 12, 9, 8, 4, 2] [13, 12, 9, 7, 6, 1] [13, 12, 9, 7, 5, 3] [13, 12, 9, 7, 4, 3] [13, 12, 9, 7, 4, 1] [13, 12, 9, 6, 5, 2] [13, 12, 9, 6, 4, 3] [13, 12, 9, 5, 4, 3] [13, 12, 9, 4, 3, 2] [13, 12, 8, 7, 6, 5] [13, 12, 8, 7, 6, 3] [13, 12, 8, 7, 6, 2] [13, 12, 8, 7, 5, 3] [13, 12, 8, 7, 5, 1] [13, 12, 8, 6, 5, 4] [13, 12, 8, 6, 3, 2] [13, 12, 8, 5, 4, 2] [13, 12, 7, 6, 5, 2] [13, 12, 7, 6, 4, 3] [13, 12, 7, 5, 4, 2] [13, 12, 6, 5, 4, 3] [13, 11, 10, 9, 8, 6] [13, 11, 10, 9, 8, 4] [13, 11, 10, 9, 8, 3] [13, 11, 10, 9, 8, 2] [13, 11, 10, 9, 7, 4] [13, 11, 10, 9, 6, 5] [13, 11, 10, 9, 6, 3] [13, 11, 10, 9, 5, 3] [13, 11, 10, 9, 4, 2] [13, 11, 10, 8, 7, 3] [13, 11, 10, 8, 6, 2] [13, 11, 10, 8, 5, 3] [13, 11, 10, 8, 4, 3] [13, 11, 10, 8, 3, 2] [13, 11, 10, 7, 6, 5] [13, 11, 10, 7, 6, 4] [13, 11, 10, 7, 6, 2] [13, 11, 10, 7, 4, 2] [13, 11, 10, 7, 3, 2] [13, 11, 10, 6, 5, 4] [13, 11, 9, 8, 7, 2] [13, 11, 9, 8, 6, 3] [13, 11, 9, 8, 5, 2] [13, 11, 9, 8, 4, 2] [13, 11, 9, 7, 6, 2] [13, 11, 9, 7, 5, 4] [13, 11, 9, 7, 5, 3] [13, 11, 9, 7, 5, 2] [13, 11, 9, 6, 5, 4] [13, 11, 9, 6, 5, 3] [13, 11, 7, 6, 5, 3] [13, 10, 9, 8, 7, 5] [13, 10, 9, 8, 7, 4] [13, 10, 9, 8, 5, 3] [13, 10, 9, 7, 5, 4] [13, 10, 9, 7, 4, 3] [13, 10, 9, 6, 5, 3] [13, 10, 8, 6, 5, 4] [13, 9, 8, 7, 6, 5] [13, 9, 8, 7, 5, 4] 13 stages, 8 taps: (132 sets) [13, 12, 11, 10, 9, 8, 7, 4] [13, 12, 11, 10, 9, 8, 7, 3] [13, 12, 11, 10, 9, 8, 7, 1] [13, 12, 11, 10, 9, 8, 6, 5] [13, 12, 11, 10, 9, 8, 6, 4] [13, 12, 11, 10, 9, 8, 6, 3] [13, 12, 11, 10, 9, 8, 6, 2] [13, 12, 11, 10, 9, 8, 6, 1] [13, 12, 11, 10, 9, 8, 5, 2] [13, 12, 11, 10, 9, 8, 4, 3] [13, 12, 11, 10, 9, 8, 3, 2] [13, 12, 11, 10, 9, 7, 6, 5] [13, 12, 11, 10, 9, 7, 6, 2] [13, 12, 11, 10, 9, 7, 5, 1] [13, 12, 11, 10, 9, 7, 3, 1] [13, 12, 11, 10, 9, 6, 5, 3] [13, 12, 11, 10, 9, 6, 5, 2] [13, 12, 11, 10, 9, 6, 4, 1] [13, 12, 11, 10, 9, 5, 3, 1] [13, 12, 11, 10, 9, 4, 3, 1] [13, 12, 11, 10, 9, 3, 2, 1] [13, 12, 11, 10, 8, 7, 6, 4] [13, 12, 11, 10, 8, 7, 6, 1] [13, 12, 11, 10, 8, 7, 5, 4] [13, 12, 11, 10, 8, 7, 4, 2] [13, 12, 11, 10, 8, 6, 5, 3] [13, 12, 11, 10, 8, 6, 5, 2] [13, 12, 11, 10, 8, 6, 3, 2] [13, 12, 11, 10, 8, 5, 4, 2] [13, 12, 11, 10, 8, 5, 4, 1] [13, 12, 11, 10, 8, 5, 3, 2] [13, 12, 11, 10, 8, 4, 3, 1] [13, 12, 11, 10, 8, 4, 2, 1] [13, 12, 11, 10, 7, 6, 5, 3] [13, 12, 11, 10, 7, 6, 2, 1] [13, 12, 11, 10, 7, 5, 4, 3] [13, 12, 11, 10, 7, 5, 3, 1] [13, 12, 11, 10, 7, 5, 2, 1] [13, 12, 11, 10, 7, 4, 3, 2] [13, 12, 11, 10, 7, 3, 2, 1] [13, 12, 11, 10, 6, 5, 3, 2] [13, 12, 11, 10, 6, 4, 3, 2] [13, 12, 11, 10, 5, 4, 3, 1] [13, 12, 11, 9, 8, 7, 6, 4] [13, 12, 11, 9, 8, 7, 5, 3] [13, 12, 11, 9, 8, 7, 5, 2] [13, 12, 11, 9, 8, 7, 4, 3] [13, 12, 11, 9, 8, 7, 3, 1] [13, 12, 11, 9, 8, 6, 5, 4] [13, 12, 11, 9, 8, 6, 5, 2] [13, 12, 11, 9, 8, 6, 5, 1] [13, 12, 11, 9, 8, 6, 4, 3] [13, 12, 11, 9, 8, 6, 4, 1] [13, 12, 11, 9, 8, 5, 4, 2] [13, 12, 11, 9, 8, 5, 3, 2] [13, 12, 11, 9, 8, 5, 3, 1] [13, 12, 11, 9, 7, 6, 5, 3] [13, 12, 11, 9, 7, 6, 5, 2] [13, 12, 11, 9, 7, 6, 4, 2] [13, 12, 11, 9, 7, 6, 4, 1] [13, 12, 11, 9, 7, 6, 3, 2] [13, 12, 11, 9, 7, 5, 4, 3] [13, 12, 11, 9, 6, 5, 4, 2] [13, 12, 11, 9, 6, 5, 4, 1] [13, 12, 11, 9, 6, 5, 2, 1] [13, 12, 11, 9, 6, 4, 3, 2] [13, 12, 11, 9, 5, 4, 3, 2] [13, 12, 11, 8, 7, 6, 4, 1] [13, 12, 11, 8, 7, 6, 3, 2] [13, 12, 11, 8, 7, 6, 3, 1] [13, 12, 11, 8, 7, 5, 3, 2] [13, 12, 11, 8, 7, 5, 2, 1] [13, 12, 11, 8, 6, 5, 3, 2] [13, 12, 11, 7, 6, 5, 4, 3] [13, 12, 11, 7, 6, 5, 4, 1] [13, 12, 11, 7, 5, 4, 3, 1] [13, 12, 10, 9, 8, 7, 6, 5] [13, 12, 10, 9, 8, 7, 6, 4] [13, 12, 10, 9, 8, 7, 6, 2] [13, 12, 10, 9, 8, 7, 5, 1] [13, 12, 10, 9, 8, 7, 4, 3] [13, 12, 10, 9, 8, 7, 4, 2] [13, 12, 10, 9, 8, 7, 3, 1] [13, 12, 10, 9, 8, 6, 5, 4] [13, 12, 10, 9, 8, 6, 4, 1] [13, 12, 10, 9, 8, 5, 4, 3] [13, 12, 10, 9, 8, 5, 3, 2] [13, 12, 10, 9, 8, 4, 3, 1] [13, 12, 10, 9, 7, 6, 5, 1] [13, 12, 10, 9, 7, 6, 4, 2] [13, 12, 10, 9, 7, 6, 4, 1] [13, 12, 10, 9, 7, 6, 3, 1] [13, 12, 10, 9, 7, 5, 3, 2] [13, 12, 10, 9, 7, 4, 3, 2] [13, 12, 10, 9, 7, 4, 3, 1] [13, 12, 10, 9, 6, 5, 4, 2] [13, 12, 10, 9, 6, 5, 4, 1] [13, 12, 10, 8, 7, 6, 5, 3] [13, 12, 10, 8, 7, 6, 5, 1] [13, 12, 10, 8, 7, 6, 4, 3] [13, 12, 10, 8, 7, 6, 4, 2] [13, 12, 10, 8, 7, 6, 3, 2] [13, 12, 10, 8, 7, 5, 4, 3] [13, 12, 10, 8, 7, 4, 3, 2] [13, 12, 10, 8, 6, 5, 4, 1] [13, 12, 10, 8, 6, 5, 3, 2] [13, 12, 10, 8, 6, 4, 3, 2] [13, 12, 10, 7, 6, 5, 4, 3] [13, 12, 10, 7, 5, 4, 3, 2] [13, 12, 9, 8, 7, 6, 5, 2] [13, 12, 9, 8, 7, 6, 5, 1] [13, 12, 9, 8, 7, 6, 4, 2] [13, 12, 9, 8, 7, 5, 4, 3] [13, 12, 9, 8, 6, 5, 4, 2] [13, 12, 9, 8, 6, 4, 3, 2] [13, 12, 8, 7, 6, 5, 3, 2] [13, 11, 10, 9, 8, 7, 5, 4] [13, 11, 10, 9, 8, 7, 5, 2] [13, 11, 10, 9, 8, 7, 4, 2] [13, 11, 10, 9, 8, 6, 5, 3] [13, 11, 10, 9, 8, 6, 5, 2] [13, 11, 10, 9, 8, 6, 4, 3] [13, 11, 10, 9, 8, 6, 3, 2] [13, 11, 10, 9, 7, 5, 4, 3] [13, 11, 10, 9, 7, 4, 3, 2] [13, 11, 10, 8, 7, 6, 5, 4] [13, 11, 10, 8, 7, 5, 4, 2] [13, 11, 10, 8, 6, 5, 4, 2] [13, 11, 9, 8, 7, 6, 5, 2] [13, 11, 9, 8, 7, 6, 4, 3] [13, 10, 9, 8, 7, 6, 5, 4] [13, 10, 9, 8, 7, 5, 4, 3] [13 stages, 10 taps: (30 sets) [13, 12, 11, 10, 9, 8, 7, 6, 5, 1] [13, 12, 11, 10, 9, 8, 7, 5, 4, 2] [13, 12, 11, 10, 9, 8, 7, 5, 3, 1] [13, 12, 11, 10, 9, 8, 6, 4, 2, 1] [13, 12, 11, 10, 9, 8, 5, 4, 3, 2] [13, 12, 11, 10, 9, 8, 5, 4, 2, 1] [13, 12, 11, 10, 9, 8, 4, 3, 2, 1] [13, 12, 11, 10, 9, 7, 6, 5, 4, 3] [13, 12, 11, 10, 9, 7, 6, 4, 3, 2] [13, 12, 11, 10, 9, 7, 6, 4, 2, 1] [13, 12, 11, 10, 9, 7, 5, 4, 3, 2] [13, 12, 11, 10, 8, 7, 6, 5, 4, 3] [13, 12, 11, 10, 8, 7, 6, 5, 3, 1] [13, 12, 11, 10, 8, 7, 6, 5, 2, 1] [13, 12, 11, 10, 8, 7, 6, 4, 3, 1] [13, 12, 11, 10, 8, 7, 5, 4, 2, 1] [13, 12, 11, 10, 8, 6, 5, 4, 3, 2] [13, 12, 11, 10, 7, 6, 5, 4, 3, 2] [13, 12, 11, 10, 7, 6, 5, 4, 3, 1] [13, 12, 11, 9, 8, 7, 6, 5, 4, 1] [13, 12, 11, 9, 8, 7, 6, 5, 2, 1] [13, 12, 11, 9, 8, 7, 5, 4, 3, 1] [13, 12, 11, 9, 8, 7, 5, 4, 2, 1] [13, 12, 11, 9, 7, 6, 5, 4, 3, 1] [13, 12, 11, 8, 7, 6, 5, 4, 3, 2] [13, 12, 10, 9, 8, 7, 6, 5, 4, 1] [13, 12, 10, 9, 8, 7, 6, 4, 3, 2] [13, 11, 10, 9, 8, 7, 6, 5, 4, 2] [13, 11, 10, 9, 8, 7, 6, 5, 3, 2] [13, 11, 10, 9, 8, 7, 6, 4, 3, 2] [13 stages, 12 taps: (2 sets) [13, 12, 11, 10, 9, 8, 7, 6, 5, 4, 3, 2] [13, 12, 11, 10, 9, 8, 7, 6, 5, 4, 2, 1] 21 Stages 29 Stages 6 Stages6 stages, 2 taps: (1 set) [6, 5] 6 stages, 4 taps: (2 sets) [6, 5, 4, 1] [6, 5, 3, 2] 14 Stages 22 Stages 30 Stages 7 Stages7 stages, 2 taps: (2 sets) [7, 6] [7, 4] 7 stages, 4 taps: (5 sets) [7, 6, 5, 4] [7, 6, 5, 2] [7, 6, 4, 2] [7, 6, 4, 1] [7, 5, 4, 3] 7 stages, 6 taps: (2 sets) [7, 6, 5, 4, 3, 2] [7, 6, 5, 4, 2, 1] 15 Stages 23 Stages 31 Stages 8 Stages8 stages, 4 taps: (6 sets) [8, 7, 6, 1] [8, 7, 5, 3] [8, 7, 3, 2] [8, 6, 5, 4] [8, 6, 5, 3] [8, 6, 5, 2] 8 stages, 6 taps: (2 sets) [8, 7, 6, 5, 4, 2] [8, 7, 6, 5, 2, 1] 16 Stages 24 Stages 32 Stages 9 Stages9 stages, 2 taps: (1 set) [9, 5] 9 stages, 4 taps: (8 sets) [9, 8, 7, 2] [9, 8, 6, 5] [9, 8, 5, 4] [9, 8, 5, 1] [9, 8, 4, 2] [9, 7, 6, 4] [9, 7, 5, 2] [9, 6, 5, 3] 9 stages, 6 taps: (14 sets) [9, 8, 7, 6, 5, 3] [9, 8, 7, 6, 5, 1] [9, 8, 7, 6, 4, 3] [9, 8, 7, 6, 4, 2] [9, 8, 7, 6, 3, 2] [9, 8, 7, 6, 3, 1] [9, 8, 7, 6, 2, 1] [9, 8, 7, 5, 4, 3] [9, 8, 7, 5, 4, 2] [9, 8, 6, 5, 4, 1] [9, 8, 6, 5, 3, 2] [9, 8, 6, 5, 3, 1] [9, 7, 6, 5, 4, 3] [9, 7, 6, 5, 4, 2] 9 stages, 8 taps: (1 sets) [9, 8, 7, 6, 5, 4, 3, 1] 17 Stages 25 Stages 25-32 Dense 10 Stages10 stages, 2 taps: (1 set) [10, 7] 10 stages, 4 taps: (10 sets) [10, 9, 8, 5] [10, 9, 7, 6] [10, 9, 7, 3] [10, 9, 6, 1] [10, 9, 5, 2] [10, 9, 4, 2] [10, 8, 7, 5] [10, 8, 7, 2] [10, 8, 5, 4] [10, 8, 4, 3] 10 stages, 6 taps: (14 sets) [10, 9, 8, 7, 5, 4] [10, 9, 8, 7, 4, 1] [10, 9, 8, 7, 3, 2] [10, 9, 8, 6, 5, 1] [10, 9, 8, 6, 4, 3] [10, 9, 8, 6, 4, 2] [10, 9, 8, 6, 3, 2] [10, 9, 8, 6, 2, 1] [10, 9, 8, 5, 4, 3] [10, 9, 8, 4, 3, 2] [10, 9, 7, 6, 4, 1] [10, 9, 7, 5, 4, 2] [10, 9, 6, 5, 4, 3] [10, 8, 7, 6, 5, 2] 10 stages, 8 taps: (5 sets) [10, 9, 8, 7, 6, 5, 4, 3] [10, 9, 8, 7, 6, 5, 4, 1] [10, 9, 8, 7, 6, 4, 3, 1] [10, 9, 8, 6, 5, 4, 3, 2] [10, 9, 7, 6, 5, 4, 3, 2] 18 Stages 26 Stages
Related Search TermsFor the benefit of those searching the Web, following are search terms related to this page:
|
| Home | | | Products | | | Literature | | | Sales | | | Support | | | Resources | | | About | | | Contact |
| ? 2002 New Wave Instruments | Page revised on 06/21/02. |